The k-means clustering algorithm aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean, serving as a prototype of the cluster. This results in a partitioning of the data space into Voronoi cells as seen below.

My application identifies cells by computing the convex
hull of all points contained within the cluster. In contrast, the Voronoi cells model the entire Euclidean plane
assuming all points exist as part of a cluster. My implementation operates primarily upon a subset of points
within the Euclidean plane and computes clusters and means dependent upon a user-specified number of clusters.
Cluster positioning will vary in my implementation as points are added and clusters are added and removed. The
cluster means can be static and given priority, however, when modeled with Voronoi cells. A demonstration of my
implementation is available in the video below.
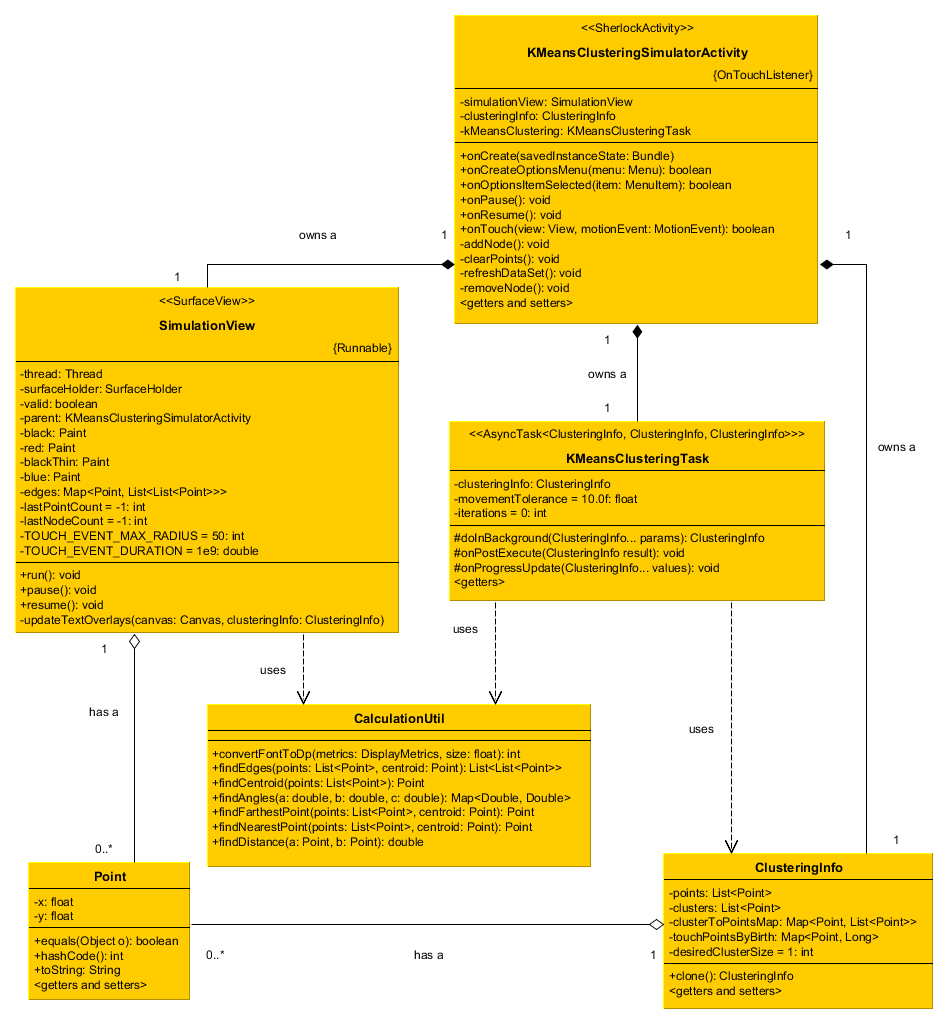
Model
View pseudocode
new SurfaceView
run():
while(valid state):
retrieve latest data set
draw Cluster means (red dots)
draw observation Points (black dots)
for each Cluster:
if(>2 Points assigned to Cluster):
if(Cluster edges not calculated OR
points.size() has changed OR
clusters.size() has changed):
compute edges
draw edges
else:
// For 2 points in cluster, mean is midpoint on connecting line
// For 1 point in cluster, mean is same as point
draw line or point
draw touch notifications per point (blue circles)
Controller pseudocode
on touch event:
in worker thread:
clear cluster means
for i in 0 to desiredClusterSize:
clusters[i] = points[i]
while(tolerance for completeness is not met):
clear all points assigned to each cluster mean
for each Point:
assign to nearest Cluster mean
for each Cluster mean:
recalculate mean
store error (distance from old to current mean)
if error > 0:
add old mean to list of moved Clusters
add new mean to list of new Clusters
for each moved Cluster:
reassign child points to new cluster mean
remove moved Cluster mean
publish progress
return data model that satisfies tolerance requirement

View Source