Click Solve to find all of the words sorted in descending order by length. Letters must be sequential neighbors (top/down, left/right, diagonals) in order to make a valid word. Edit the letters manually or refresh the page to receive a new random ordering.

Finding all of the words through an exhaustive search is not possible due to the high number of permutations. The requirement that each successive letter within a word is a neighbor in the grid reduces the number of permutations, but it is still quite large. Additionally, words can vary in length from 1 to 16 characters and each of those permutation sets need to be counted. The upper bound without neighbor restrictions is thus:

            >>> def factorial(x):
                    product = 1
                    for i in range(1, x+1):
                        product *= i
                    return product
            
            >>> sum([factorial(x) for x in range(1, 17)])
            22324392524313L

Making sense of this number, there are 16 possible words of length 1, 16 * 15 = 240 words of length 2, 16 * 15 * 14 = 3,360 words of length 3, and so on until reaching 16! = 20,922,789,888,000 words of length 16. This results in over 22 trillion total permutations. A standard dictionary list will contain well over 100,000 words for this type of game. A clever method is needed to programmatically find all of the words as the combinations are just too plentiful to use a computationally expensive algorithm.

One problem that arises is determining if a String exists in a Collection as a partial match. To illustrate this problem, given myList = ["Read", "Reading", "Reader"], is there a partial match for segment = "Rea"? The HashSet will return false when asked if myList.contains(segment) as expected because it only computes a hashCode for the entire String. A full match is computationally inexpensive as a HashSet will provide O(1) complexity in the best case scenario. However, a partial match determination will require each element to be inspected O(n), substring computed O(n), and an equals evaluation performed at each step O(n).

This problem was solved using a custom Trie data structure that allows for very fast retrieval of desired information. We want to know if a test word appears within a very large collection of reference words, both partially (so we know if we should continue down this permutation path or not), and fully (so we know when to identify this permutation as a valid word).

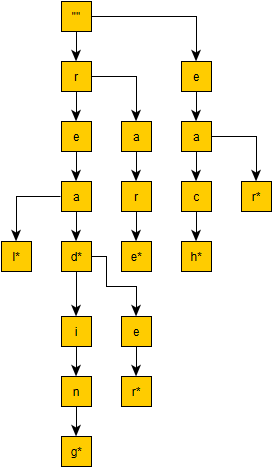
The visually represented Trie data structure to the left contains these words: ["reading", "reader", "read", "real", "rare", "each", "ear"]. Each letter represents a TrieNode instance. A terminating letter, which is one that ends a valid word, is designated with an asterisk. Additional letters may follow a terminating letter since there are often many variations on a root word.

This tree will become very wide as additional words are added. This is desirable because the worst case scenario in determining if a test word is contained within the Trie is now limited in work according to the depth, which will correspond to the length of the longest word. A HashMap<String, TrieNode> exists at each node to contain the children. Since searching a HashMap has O(1) complexity, the contains and containsPartial methods for the Trie in the average case will be mean word length * O(1), which can just be simplified to O(1) since the mean word length doesn't necessarily change as the word list grows.